Как найти центр круга с помощью циркуля

При изготовлении или обработке деталей из древесины в некоторых случаях требуется определить, где находится их геометрический центр. Если деталь имеет квадратную или прямоугольную форму, то сделать это не представляет никакого труда. Достаточно соединить противоположные углы диагоналями, которые при этом пересекутся точно в центре нашей фигуры.

Для изделий, имеющих форму круга, такое решение не подойдет, поскольку у них нет углов, а значит и диагоналей. В этом случае необходим какой-то другой подход, основанный на иных принципах.

И они существуют, причем в многочисленных вариациях. Одни из них достаточно сложные и требуют нескольких инструментов, другие – легкие в реализации и для их осуществления не нужен целый набор приспособлений.

Сейчас мы рассмотрим один из самых простых способов нахождения центра круга с помощью только обычной линейки и карандаша.

Последовательность нахождения центра круга:

1. Для начала нам надо вспомнить, что хордой называют прямую линию, соединяющую две точки окружности, и не проходящую через центр круга. Воспроизвести ее совсем нетрудно: необходимо лишь положить линейку на круг в любом месте так, чтобы она пересекала окружность в двух местах, и провести карандашом прямую линию. Отрезок внутри окружности и будет хордой.

В принципе можно обойтись одной хордой, но мы для повышения точности установления центра круга нарисуем хотя бы пару, а еще лучше – 3, 4 или 5 разных по длине хорд. Это позволит нам нивелировать погрешности наших построений и точнее справиться с поставленной задачей.

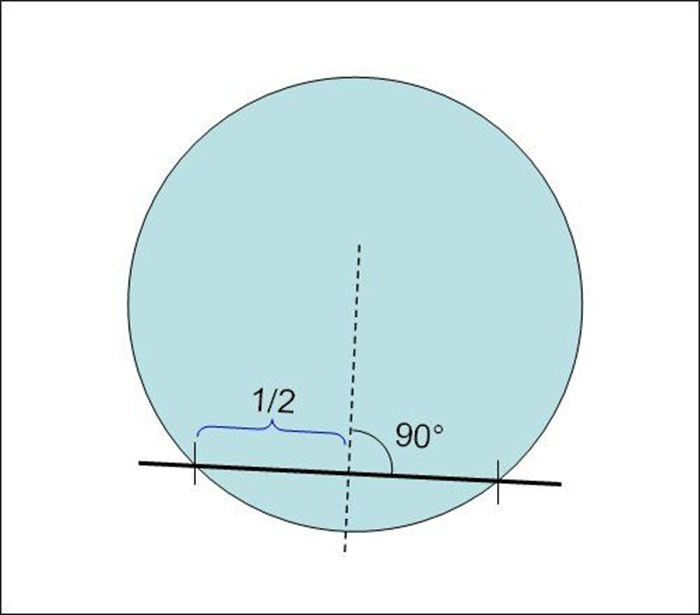
2. Далее, используя ту же линейку, находим середины воспроизведенных нами хорд. Например, если общая длина одной хорды равна 28 см, то ее центр будет находиться в точке, которая отстоит по прямой от места пересечения хорды с окружностью на 14 см.

Определив таким способом центры всех хорд, проводим через них перпендикулярные прямые, используя, например, прямоугольный треугольник.

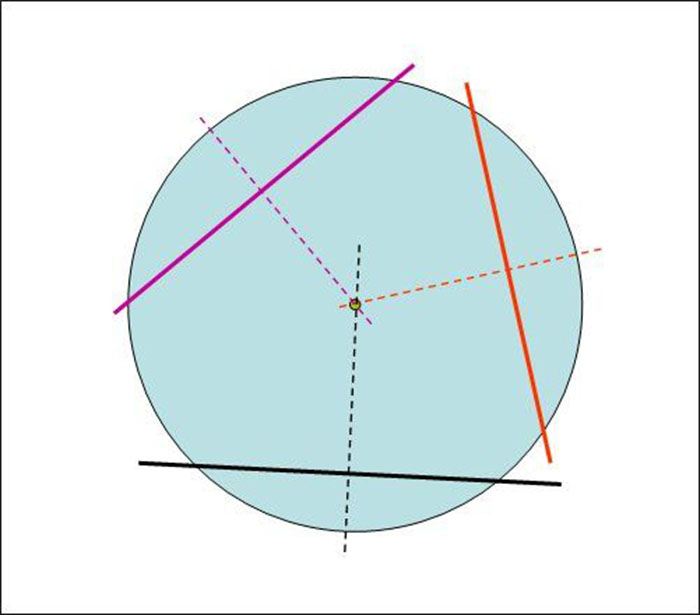
3. Если мы теперь продолжим эти перпендикулярные к хордам прямые в направление к центру окружности, то они пересекутся примерно в одной точке, которая и будет искомым центром круга.

4. Установив местоположение центра нашего конкретного круга, мы можем использовать этот факт в различных целях. Так, если в эту точку поместить ножку столярного циркуля, то можно начертить идеальную окружность, а затем и вырезать круг, используя соответствующий режущий инструмент и определенную нами точку центра круга.

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №1 с. Александров – Гай

Исследовательская работа по математике:

Подготовил: Амиров Марат, ученик 6 «а»

класса МБОУ СОШ №1 с. Александров – Гай

Руководитель: , учитель математики МБОУ СОШ №1 с. Александров — Гай

С. Александров – Гай

Глава 1 «Способы нахождения окружности» …………………………………..4

Глава 2 «Практическая часть»…………………………………………………..6

Список литературы и источников………………………………………………12

Окружность — совокупность точек, находящихся на равном расстоянии от одной точки, называемой центром. Однако в тех случаях, когда вам дана одна только окружность, нахождение ее центра может быть непростой задачей. Поэтому цель моей исследовательской работы: изучить способы определения центра окружности. Исходя из цели были поставлены задачи:

— найти самый простой способ определения центра окружности;

— сравнить несколько способов определения центра окружности;

— практические способы определения центра окружности.

Актуальность ислледовательской работы заключается в том, что в повседневной жизни людей часто приходится находить центр окружности, но не каждый знает как это правильно сделать. Поэтому изучение данной темы поможет найти правильное решение проблемы и определить оптимальный вариант для человека любой професии.

При написании исследовательской работы были использованны электронные источники и литература. Электронные источники помогли найти теоретический материал по теме, а учебники по математике были использованны для подбора задач и практической части работы.

Глава 1. Способы нахождения центра окружности.

1.Самый простой способ нахождения центра окружности — согнуть лист бумаги, на котором она начерчена, следя на просвет, чтобы окружность оказалась сложена точно пополам. Полученная линия сгиба будет одним из диаметров заданной окружности. Затем лист можно согнуть в другом направлении, получив тем самым второй диаметр. Точка их пересечения и будет

центром окружности.

2. Для того чтобы найти центр окружности, надо сначала вписать ее в квадрат. То есть все стороны четырехугольника должны касаться круга. Для этого проведите с помощью линейки четыре ровные линии. Теперь соедините по диагонали два противоположных угла. Следите за тем, чтобы линия разбивала угол квадрата на две равные части. Соедините прямыми все 4 угла квадрата. Точка пересечения данных прямых и будет центром окружности.

3. Для любого треугольника центр описанной окружности находится в точке пересечения срединных перпендикуляров. Если этот треугольник — прямоугольный, то центр описанной окружности всегда совпадает с серединой гипотенузы. Следовательно, если вписать в окружность прямоугольный треугольник, то его гипотенуза будет диаметром этой окружности.

В качестве трафарета для этого способа подойдет любой прямой угол — школьный или строительный угольник, или просто лист бумаги. Поместите вершину прямого угла в любую точку окружности и сделайте отметки там, где стороны угла пересекают границу круга. Это конечные точки диаметра.
Тем же способом найдите второй диаметр. В точке их пересечения

4.На круглую деталь накладываем лист бумаги так, что бы один его угол находился на окружности или крае круга. И отмечаем точки, где лист соприкасается другими краями с кругом. Отмечаем эти точки.

Проводим прямую линию между отмеченными точками. Расстояние между ними является диаметром этого круга. Обрезаем лишнюю бумагу и проводим на детали прямую линию — диаметр.

Достаточно переместить наш треугольник в другое положение и нарисовать еще один диаметр круга, как тут же в точке пересечения диаметров мы и получим искомый центр окружности…

5. Диаметр и радиус окружности.

Диаметр окружности — это отрезок прямой, соединяющий пару наиболее удаленных друг от друга точек окружности, проходящий через центр окружности. Слово «диаметр» произошло от греческого слова «diametros» — поперечный. Обычно диаметр обозначается латинской буквой D или значком Ø.

Диаметр можно найти по формуле: D = 2R, где диаметр равен удвоенному радиусу окружности.
Радиус — расстояние от центра до любой точки окружности. Обозначается латинской R.
Если известен радиус окружности, допустим, он равен 8 см, то значит D = 2 * 8 = 16 см.

Радиус окружности определяется по формуле : R=D:2

» w />
Глава 2 «Практическая часть»

1) Прямой угол детали закруглен дугой радиуса R

Для решения задачи с центром в вершине прямого угла проводят окружность радиуса R, которая пересекает стороны прямого угла в точках А и В.

С центрами в точках А и В строят еще две окружности радиуса R; С – их точка пересечения. Дуга окружности радиуса R с центром в точке С и будет искомым закруглением.

Произвольный угол детали закруглить дугой радиуса R

Решение: На расстоянии R от сторон угла проводят соответствующие параллельные им прямые. О — их пересечение. Затем строим окружность с центром О, радиуса R

Даны две параллельные прямые и точка А между ними. Как построить окружность, касающуюся данных прямых и проходящих через данную точку?

1) Построим любую окружность, касающуюся двух прямых (центр окружности находим, разделив ее пополам)

2) Проведем через А прямую, равную данным. Она пересечет построенную окружность в точках В и С. Перед ними центр построенной окружности на АВ или АС.

Задачи на построение технического рисунка

Как при помощи слесарного разметочного угольника измерить недоступный диаметр круглой детали.

Можно ли прибором, изображенным на рисунке одним прикладыванием найти центр круга?

«Как найти центр окружности?» — вопрос, на который мне пришлось ответить в ходе исследования. Таким образом, я нашел несколько способов построения центра окружности: 1) центроискатель — прямой угол. Принцип работы: вписанный угол опирается на диаметр. 2) Центроискатель — угол с биссектрисой. Принцип работы: диаметр окружности лежит на биссектрисе угла, описанного около этой окружности.3)Центроискатель – пара взаимно перпендикулярных прямых. Принцип работы: диаметр, проведенный в точку касания, перпендикулярен касательной. 4)Центроискатель – пара взаимно перпендикулярных прямых. Принцип работы: хорда, перпендикулярная другой хорде и проходящая через ее середину, есть диаметр.

Соответственно цель моей работы достигнута: изучив несколько способов нахождения центра окружности возможно из каждого выбрать оптимальный вариант.

О, математика земная!
Гордись, прекрасная, собой,
Ты всем наукам мать родная,
И дорожат они тобой.

Твои расчеты величаво
Ведут к планетам корабли
Не ради праздничной забавы,
А ради гордости Земли!

Список использованной литературы и источников

1.Журнал «Математика в школе» №20 1989г.

Добрый день коллеги. Что бы найти радиус окружности с помощью линейки и циркуля много времени не нужно. Вспомним школьные годы. Для тех, кто запамятовал или прогуливал будет полезен этот урок.

Все легко. Но случается, когда очевидное произносишь вслух, тогда вдруг понимаешь: «- Я так и думал. Что такое диаметр окружности я знал. Просто не помню…».

Существуют разные подходы.

• Можно найти диаметр круга через вычисления.
• Найти цент окружности с помощью угольника.
• Решить с помощью листа ватмана (важно, чтобы был лист с 90 градусными углами).
• А можно применив циркуль и линейку.

Рассмотрим простой способ (один из…), как найти диаметр окружности с помощью линейки и циркуля.

Здесь чистая геометрия. А эта наука идет рядом с живописью, с архитектурой.

Для чего это художникам?

Работа с цветным стеклом. В церквях окна с раскрашенными кусочками стекла составляют картины. Делая такие витражи без точных вычислений не обойтись. Каждый из кусочков нужно точно вырезать и поставить в определенную ячейку. Поэтому и здесь пригодиться наш метод.

Представим, что мы расписываем стену, у нас имеется круглый трафарет, но вот центра нет. А нам жизненно необходимо его определить и точно прикладывать к определенным точкам нашей композиции на стене.

Может мы мастера по дереву. Делаем резной круглый стул или стол. В средине необходимо просверлить или нарисовать узор.

Очень тяжелая работа роспись на потолке. Формы разные. Когда начинаем с начала, то средина будет. Когда панно переделываем, то круг имеется, но центр нужно найти. С размерами необходимо будет повозиться, но это второй вопрос.

Возможно найти радиус круга, центр путем подбора, но это долго и не эффективно.

На видео ниже детально описано как найти центр.

Как найти центр окружности

Рассмотрим в картинках, как найти радиус окружности

Что такое диаметр окружности многие знают.

Линия, нарисованная через центр окружности и будет диаметр. Радиус круга — это его половина (для того, кто не помнит).

Дана окружность зеленый цвет.

На теле зеленого круга ставим случайно точку A, и вокруг нее описываем круг фиолетового цвета.

Ставим еще одну точку B. Описываем второй круг.

Проведя через пересечения фиолетовых окружностей прямую, получаем диаметр зеленого круга C D.

Эту же процедуру проводим с желтыми объектами. Только их центрами будут точки C D.

Проведя через пересечения желтых объектов прямую, получим очередной диаметр перпендикулярный первому. Их пересечение будет центром зеленого с точкой O.

Важно, чтобы фиолетовые круги были одинаковы, а по размеру чуть больше зеленого.

К желтым окружностям это тоже относится.

Этим не хитрым способом получим центр, что поможет без задержек выполнить заказ.

Человек на рисунке часто окружен архитектурными объектами. Без точных вычислений определить геометрию окружения, уходящую в перспективу, не выйдет. В такие моменты и нужны знания геометрии.

Построить среду обитания не сложно. Имея знания, подобная задача не будет трудной.

Все художники (без исключения) пользуются построением.

В уроках рисования на нашем сайте можно онлайн узнать ответы на разные вопросы.

В курсе по рисунку собраны уроки перспективы, тона, построения, композиции и разные хитрости.

Посмотреть заметки о делении круга на семь частей, на пять, двенадцать…

Внеклассный урок — Окружность

Окружность

Окружность – это фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки.

 

Основные понятия:

Центр окружности – это точка, равноудаленная от точек окружности.

Радиус – это расстояние от точек окружности до ее центра (равен половине диаметра, рис.1).

Диаметр – это хорда, проходящая через центр окружности (рис.1).

Хорда – это отрезок, соединяющий две точки окружности (рис.1).

Касательная – это прямая, имеющая только одну общую точку с окружностью. Проходит через точку окружности перпендикулярно диаметру, проведенному в эту точку (рис.1).

Секущая – это прямая, проходящая через две различные точки окружности (рис.1).

Единичная окружность – это окружность, радиус которой равен единице.

Дуга окружности – это часть окружности, разделенная двумя несовпадающими точками окружности.

1 радиан – это угол, образуемый дугой окружности, равной длине радиуса (рис.4).
1 радиан = 180˚ : π ≈ 57,3˚

Центральный угол – это угол с вершиной в центре окружности. Равен градусной мере дуги, на которую опирается (рис.2).

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Равен половине градусной меры дуги, на которую опирается (рис.3).

  Две окружности, имеющие общий центр, называются концентрическими.

Две окружности, пересекающиеся под прямым углом, называются ортогональными.

 

Длина окружности и площадь круга:

Обозначения:
Длина окружности – C
Длина диаметра – d
Длина радиуса – r

Значение π:
Отношение длины окружности к длине ее диаметра обозначается греческой буквой π (пи).

π = 3,1416

Или:

π = 3,14

Или:

       22
 π = —
        7

Формула длины окружности:

C = πd, или C = 2πr

 

Формулы площади круга:

S = πr²

      C · r
S = ——
          2

        π · D²
S = ———
           4

 

Площадь кругового сектора и кругового сегмента.

Круговой сектор – это часть круга, лежащая внутри соответствующего центрального угла. Формула площади кругового сектора:                                                                         πR2                                                               S = ——— α                                                                         360 где π – постоянная величина, равная 3,1416; R – радиус круга; α – градусная мера соответствующего центрального угла. Круговой сегмент – это общая часть круга и полуплоскости. Формула площади кругового сегмента:                                                                         πR2                                                               S = ——— α  ±  SΔ                                                                         360 где α – градусная мера центрального угла, который содержит дугу этого кругового сегмента; SΔ  — площадь треугольника с вершинами в центре круга и в концах радиусов, ограничивающих соответствующий сектор. Знак «минус» надо брать, когда α < 180˚, а знак «плюс» надо брать, когда α > 180˚.

 

Уравнение окружности в декартовых координатах x, y c центром в точке (a;b):

(x – a)² + (y – b)² = R²

 

Окружность, описанная около треугольника (рис.4).

Если от середины каждой из сторон треугольника провести перпендикуляры, то точка их пересечения будет центром окружности, описанной около этого треугольника.

 

Окружность, вписанная в треугольник (рис.5).

Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис этого треугольника.

 

Углы, вписанные в окружность (рис.3).

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность.

Угол, вписанный в окружность, равен половине соответствующего центрального угла.

 

Основные понятия:

Угол делит плоскость на две части. Каждая из этих частей называется плоским углом.

Плоские углы с общими сторонами называются дополнительными.

Плоский угол с вершиной в центре окружности называется центральным углом (рис.2)

Пропорциональность отрезков хорд и секущих окружности.

Если хорды AB и CD окружности пересекаются в точке S, то AS · BS = CS · DS. (рис.6)

 

Если из точки P к окружности проведены две секущие, пересекающие окружность соответственно в точках A, B и C, D, то AP · BP = CP · DP (рис.7)

 

Частные случаи и формулы:

1) Из точки C, находящейся вне окружности,  проведем касательную к окружности и обозначим точку их соприкосновения буквой D.

Затем из той же точки C проведем секущую и точки пересечения секущей и окружности обозначим буквами А и B (рис.8).

В этом случае:

CD² = AC · BC

 

2) Проведем в окружности диаметр AB. Затем из точки C, находящейся на окружности, проведем перпендикуляр к этому диаметру и обозначим получившийся отрезок CD (рис.9).

В этом случае:

CD² = AD · BD.

Ответы Mail.ru: что такое центр окружности?

Точка, от которой любые две данные точки, принадлежащие окружности, удалены на равные расстояния.

Это такая точка.

точка равноудаленная от всех других точек

Точка, в которую ставится ножка циркуля для того, чтобы нарисовать окружность.

Центр окр. — это точка равноудаленная от сторон окр.

центр окружности- точка лежащая в плоскости окружности и равноудаленная от любой точки принадлежащий окружности (примечание: «точка лежащая в плоскости окружности» без этого слова получится прямая проходящяя через центр окружности и перпендикулярная окружности)

Ответе плиз. Что такое определение? Дайте определение окружности, что такое центр , радиус , хорда и диаметр окружности

ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.

ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.

Окружностью называется геометрическое место точек равноудаленных от данной точки (центра окружности) на заданное расстояние (радиус окружности) Радиус — отрезок, соединяющий центр окружности с любой её точкой. Кругом называется геометрическое место точек удаленных от данной точки (центра круга) неболее чем на заданное расстояние (радиус круга) Секущая — это прямая, имеющая с окружностью две общие точки (на рисунке 1 показана секущая l ). Отрезок секущей, лежащий внутри окружности, называется хордой (на рисунке 1 показана хорда АВ). Итак, Хордой называется отрезок соединяющий две произвольные (несовпадающие) точки окружности. Части, на которые хорда разбивает круг , называются сегментами. В случае, когда хорда совпадает с диаметром, эти сегменты превращаются в полукруги. Диаметром называют хорду, проходящую через центр окружности. Сектором круга называют часть круга, ограниченная двумя его радиусами и дугой окружности, соединяющей концы этих радиусов

ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.

ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.

ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.

ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.

Определение — объяснение понятия, опирающееся на начальные понятия (например, понятие «точка») или на определенные ранее. Окружность — это геометрическое место точек плоскости, равноудаленных от одной точки плоскости. Центр окружности — точка плоскости, равноудаленная от всех точек окружности. Радиус окружности — равные отрезки, соединяющие центр с точками окружности. Хорда — отрезок, соединяющий любые две точки окружности. Диаметр окружности — хорда, проходящая через центр.

ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.

центр круга — это… Что такое центр круга?

центр круга — skritulio centras statusas T sritis fizika atitikmenys: angl. center of circle vok. Kreismittelpunkt, m rus. центр круга, m pranc. centre du cercle, m …   Fizikos terminų žodynas

эгоцентризм (лат. EGO – и CENTRUM – центр круга) — черта личности, проявляющаяся в преувеличенном подчеркивании своего Я , крайнем эгоизме, неспособность индивида, сосредоточенного преимущественно на собственных интересах, изменить свою позицию по отношению к чуткому мнению, представлению даже… …   Энциклопедический словарь по психологии и педагогике

центр — а; м. [от греч. kentron острие, средоточие] 1. Матем., физ. Точка пересечения каких л. осей, линий в фигуре, точка сосредоточения каких л. отношений, сил в теле. Ц. линзы. Ц. окружности. Ц. симметрии. Ц. тяжести (также; самое основное, суть).… …   Энциклопедический словарь

ЦЕНТР — муж., лат. средоточие, остие, осен, остен. Центр круга, шара. Круги одного или общего центра, из одной точки начерченные. | Приблизительная средина плоскости. Губернский город стоит в центре губернии. * Центр торговли, где она сосредоточена.… …   Толковый словарь Даля

ЦЕНТР — (лат. centrum центр круга) ..1) середина2)] Населенный пункт (напр., областной центр)3) Место сосредоточения какой либо деятельности, органов управления, организаций и пр …   Большой Энциклопедический словарь

ЦЕНТР — (от лат. centrum центр круга и греч. kentron срединная точка, средоточие) англ. centre; нем. Zentrum. 1. Средняя часть Ч. Л., середина. 2. Место сосредоточения к. л. деятельности, управления и т. п. (промышленный Ц.). 3. Город, крупный населенный …   Энциклопедия социологии

ЦЕНТР — (от лат. centrum центр круга и греч. kentron срединная точка, средоточие) англ. centre; нем. Zentrum. 1. Средняя часть Ч. Л., середина. 2. Место сосредоточения к. л. деятельности, управления и т. п. (промышленный Ц.). 3. Город, крупный населенный …   Толковый словарь по социологии

ЦЕНТР — (лат. centrum, от греч. kentron). 1) средоточие, средина круга, шара и проч. 2) политическая партия в Германии, в качестве протеста против дальнейшего развития германского союза во имя независимости церкви от государственной власти. Словарь… …   Словарь иностранных слов русского языка

ЦЕНТР — несет в себе понятие смыслового центра, центра мироздания и мистического центра, символизирующего высший принцип Вселенной. Смысловой центр это основное ядро той или иной теории, того или иного учения, системы взглядов, комплекса… …   Символы, знаки, эмблемы. Энциклопедия

РАДИУС КРУГА — линия, соедин. центр круга с к. л. точк. его окружности. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907 …   Словарь иностранных слов русского языка

ТОРГОВЫЙ ЦЕНТР — (от лат. centrum центр круга) группа разнородных торговых предприятий, сосредоточенных в одном месте, функционирующих и управляемых как единый, целостный объект. Торговый центр способен обслуживать целую торговую зону всеми необходимыми видами… …   Экономический словарь